The algorithm is based on libtess2 here and we optimizated some implementation and fixed some bugs.
The differents between our algorithm and libtess2’s algorithm:
- We change the coordinate system and the sweep direction (sweep line by horizontal here).
- We need not project the vertices because our graphic engine is 2d, so our algorithm will be faster.
- We processed more cases of the intersection with some numerical errors, so our algorithm will be more stable.
- We change the algorithm of comparing the active edge and make it more stable for numerical errors.
- We optimizate the algorithm of merging into the convex polygon from the triangulated mesh.
- We have not counted the vertices for each region, so it will be faster than libtess2.
(you can see libtess2/alg_outline.md if want to known more details of algorithm.)
There are four stages to the algorithm:
- Build a mesh (DCEL, be similar to quad-edge) from polygon.
- Tessellate the mesh into the monotone regions if the polygon is concave.
- Triangulate the monotone regions.
- Merge the triangulated regions into the convex regions.
There are seven stages to the tessellation algorithm:
- Simplify the mesh and process some degenerate cases.
- Build a vertex event queue and sort it (uses the priority queue with min-heap).
- Build an active edge region list and sort it (uses the partial insertion sort).
- Sweep all events from the event queue using the Bentley-Ottman line-sweep algorithm and calculate the intersection and winding number.
- We need fix it if the intersection with numerical errors violate the mesh topology or active edge list ordering.
- Process some degenerate cases for the mesh faces which were generated when we fixed some cases.
- Get the monotone regions with the left face marked “inside”
The triangulation test result:
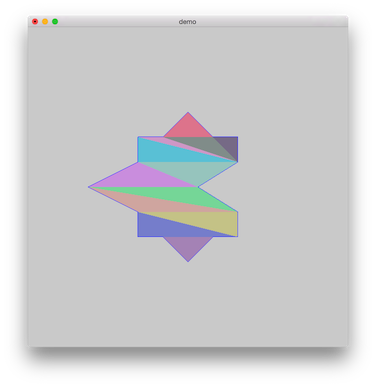
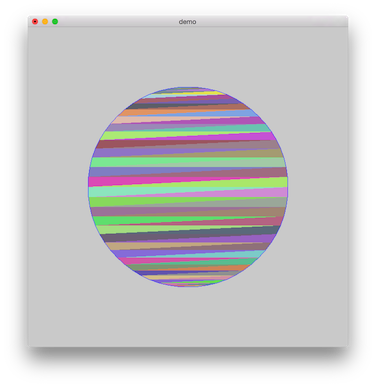
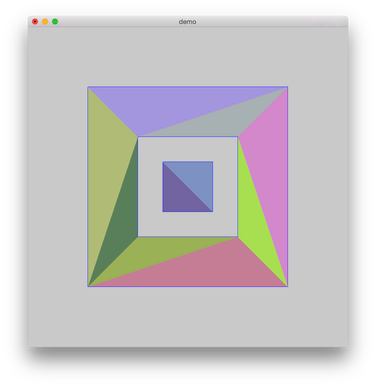
The drawing result with opengl(60 fps on my mac pro):
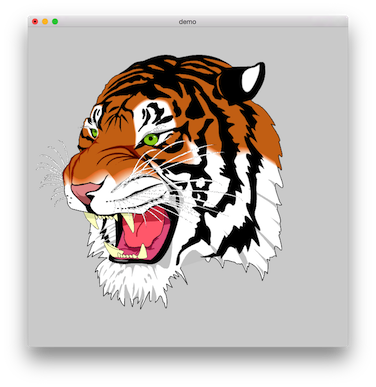
Please refer to the source code monotone.c if you want to know more verbose monotone algorithm implementation.
And the tessellator interfaces usage from gbox/gl/render.c:
static tb_void_t gb_gl_render_fill_convex(gb_point_ref_t points, tb_uint16_t count, tb_cpointer_t priv)
{
// check
tb_assert(priv && points && count);
// apply it
gb_gl_render_apply_vertices((gb_gl_device_ref_t)priv, points);
#ifndef GB_GL_TESSELLATOR_TEST_ENABLE
// draw it
gb_glDrawArrays(GB_GL_TRIANGLE_FAN, 0, (gb_GLint_t)count);
#else
// the device
gb_gl_device_ref_t device = (gb_gl_device_ref_t)priv;
// make crc32
tb_uint32_t crc32 = 0xffffffff ^ tb_crc_encode(TB_CRC_MODE_32_IEEE_LE, 0xffffffff, (tb_byte_t const*)points, count * sizeof(gb_point_t));
// make color
gb_color_t color;
color.r = (tb_byte_t)crc32;
color.g = (tb_byte_t)(crc32 >> 8);
color.b = (tb_byte_t)(crc32 >> 16);
color.a = 128;
// enable blend
gb_glEnable(GB_GL_BLEND);
gb_glBlendFunc(GB_GL_SRC_ALPHA, GB_GL_ONE_MINUS_SRC_ALPHA);
// apply color
if (device->version >= 0x20) gb_glVertexAttrib4f(gb_gl_program_location(device->program, GB_GL_PROGRAM_LOCATION_COLORS), (gb_GLfloat_t)color.r / 0xff, (gb_GLfloat_t)color.g / 0xff, (gb_GLfloat_t)color.b / 0xff, (gb_GLfloat_t)color.a / 0xff);
else gb_glColor4f((gb_GLfloat_t)color.r / 0xff, (gb_GLfloat_t)color.g / 0xff, (gb_GLfloat_t)color.b / 0xff, (gb_GLfloat_t)color.a / 0xff);
// draw the edges of the filled contour
gb_glDrawArrays(GB_GL_TRIANGLE_FAN, 0, (gb_GLint_t)count);
// disable blend
gb_glEnable(GB_GL_BLEND);
#endif
}
static tb_void_t gb_gl_render_fill_polygon(gb_gl_device_ref_t device, gb_polygon_ref_t polygon, gb_rect_ref_t bounds, tb_size_t rule)
{
// check
tb_assert(device && device->tessellator);
#ifdef GB_GL_TESSELLATOR_TEST_ENABLE
// set mode
gb_tessellator_mode_set(device->tessellator, GB_TESSELLATOR_MODE_TRIANGULATION);
// gb_tessellator_mode_set(device->tessellator, GB_TESSELLATOR_MODE_MONOTONE);
#endif
// set rule
gb_tessellator_rule_set(device->tessellator, rule);
// set func
gb_tessellator_func_set(device->tessellator, gb_gl_render_fill_convex, device);
// done tessellator
gb_tessellator_done(device->tessellator, polygon, bounds);
}